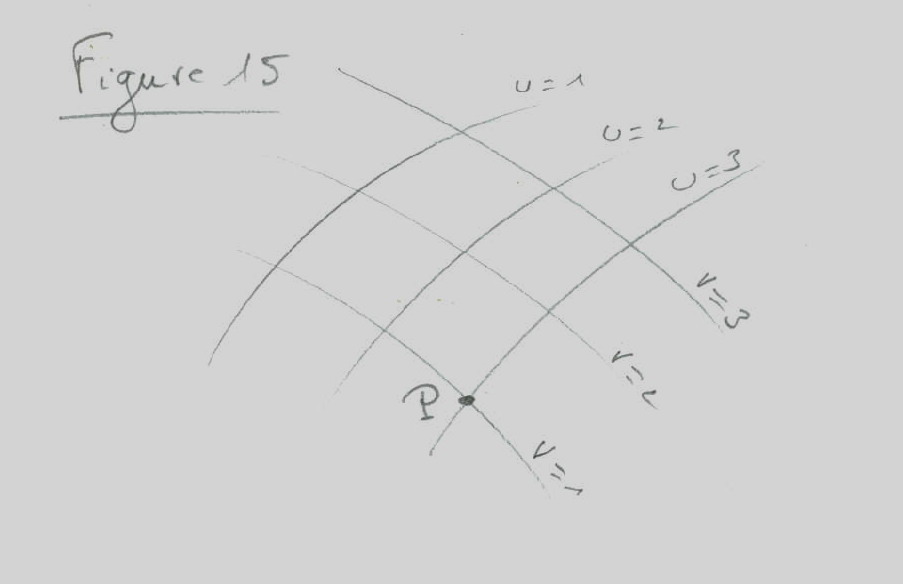
Let us consider a system of arbitrary curves u (u-curves) drawn on a flat plane (see figure 15). We distinguishes each of them by a different number so that we have, for instance, the curves u = 1, u = 2, u = 3.Between the curves u = 1 and u = 2 there are an infinite number of curves which correspond to real numbers between 1 and 2. As we see there is an infinite number of curves u that covers the whole surface of the plane. The u-curves do not intersect each other and only one curve u passes through each point of the surface of the plane. As a consequence, a well-defined value of u belongs to every point of the plane.
Let us consider a system of v-curves draw on the same plane (see figure 15). Again only one value of v belongs to each point. Now to each point of the plane such as P correspond a well-defined value of u and another well-defined value of v. We will call these two numbers the Gaussian coordinates of the point (in the case of P, u = 3 and v = 1).
Two points close to each other on the surface have the co-ordinates:
P : u, v
P': u+du, v+dv (du and dv are small numbers)
According to gauss the distance ds between P and P' is found from the following
equation:
ds² = g11*du² + 2g12*du*dv + g22*dv²
g11, g12 and g22 are values depending on u and v.
If the point of the plane form a Euclidian continuum it is possible to
draw the u and v curves and to attach number to them so that we have: ds²
= du²+dv²
In this case the curves u and v are straight lines perpendicular to each
other as in the Euclidean geometry. Here, and only here, the Gaussian co-ordinates
are identical to the Cartesian ones.
Until now we have only considered a two-dimension continuum but the Gaussian
method is applicable to a continuum of 3, 4 or more dimensions. A four dimensional
continuum can be represented as follow:
With every point of the continuum we associate four arbitrary numbers x1,
x2, x3, x4 known as the co-ordinates of a point P. An adjacent point P'
-distant ds from P- would have adjacent values for it co-ordinates and:
Ds² = g11*dx1² + 2g12*dx1*dx2 + … + g44*dx4²
Again g11, etc. have values depending on the position of P in the continuum.
When, and only when the continuum is Euclidean it is possible to associate
the co-ordinates x1, x2, x3, x4 so that: ds² = dx1² + dx2²
+ dx3² + dx4²
However the previous Gauss treatment only works when small regions of the
continuum are Euclidean.