As we will see the theories of relativity are applicable to the big structures of the universe but, as they do not take into consideration the uncertainty principle (see part 6) they are not yet perfect. The differences between the predictions of the theories of relativity and the experimental data are small because, on a large scale at least, the effects of gravity are small. The exceptions are the black holes and the big bang where gravity is extremely strong. A complete and consistent theory that unifies general relativity and quantum mechanics does not exist yet, although scientists -including Einstein- have been working on it since the 1920s.
Our personnel notion of time and space are very important in our everyday life. They are used to order things and events in our environment, and are necessary to understand science and philosophy. All laws of physics require our conception of space and time for their formulation and understanding. But relativity changed all of our concepts that until then had been accepted as true and universal.
Classical physics is based on two main concepts:
- Space is absolute and three-dimensional, independent of the material bodies
it contains, and it obeys the laws of Euclidean geometry.
- Time is a separate and absolute dimension that runs at a fixed rate.
These classical concepts have their origin in Greek thought and philosophy: on the base of accepted axioms it is possible to find theorems by sheer deduction. As a result geometry, a science thought to be of divine origin, but also the combination of logic and beauty, was at the core of Greek philosophy. Its mathematical theorems were thought to be the expression of eternal and exact truths about the real world. Euclid's "Elements" was the standard textbook until the beginning of the 19th century; then came Einstein who demonstrated that geometry is not inherent in nature, but is imposed on it by the human mind.
Eastern philosophers have been maintaining for a long time that space and
time are construction of the mind. For instance, time in the east was not
seen as absolute, it was not the ultimate truth. Their philosophers treated
them like any other intellectual concepts: relative, limited, and illusory.
In other words, the eastern philosophers' mind was better prepared to receive
and accept the concepts of relativity than their colleagues from the west.
The basic concepts that emerged from the theory of relativity are that time and space measurements are relative. Already before Einstein it was known that the position of any object in space could only be defined relative to some other object with the use of three co-ordinates, the point from which they originate being the "location" of the observer. On the other hand, time was considered as absolute, that is independent of the observer. Einstein was the first to recognise that time too is relative and dependant on the observer. Until Einstein people were only aware of velocities much lower than the speed of light and, if only for this reason, they thought that it was possible to arrange events in a unique sequence. But the speed of light, although very high, is limited and it is wrong to say that we see events the moment they occur since it takes time for light to travel from the event to the observer. As a consequence, observers moving at different velocities will order events differently in time.
The relativity of time also throws away the Newtonian's concept of absolute space. Like light, space is also a relative concept depending on the velocity of motion of the observers. An event that happens at a well defined time for one observer can be seen to happen before or after for another, and this excludes the possibility to talk about "the universe at a given instant". Space too depends on the position and motion of the observer.
In conclusion, relativity shows that all measurements involving space and time are not absolute; this obliges us to abandon the classical concepts of an absolute space and an absolute time.
In classical physics objects such as rods have the same length whether they are in movement or at rest. Relativity theory shows that this is not true, the length of a rod changes according to its speed in relation to an observer with the moving object contracting in the direction of the movement. A rod has its maximum length at rest, it decreases with speed, and would have a zero length if it could travel at the speed of light. In consequence asking what is the real length of a rod has no sense anymore.
And what is true for length is also true for time intervals. They depend
on the frame of reference but, in contrary to the length of a rod, time
intervals become longer as the velocity relative to the observer increases.
In clear, clocks in motion run slower, time slow down. This is true for
mechanical clocks, atomic clocks etc. In the same way the human heartbeat,
blood flow, brainwaves, etc slow down with increasing speed. All this seems
strange to us because we cannot experience the four-dimensional space-time
world with our senses. All we can see is its three-dimensional image that
changes with the frame of reference.
The general theory of relativity is an extension of the special theory in
the sense that it includes gravity. The first effect of gravity is to make
space-time curved, although it is difficult to visualise what that really
means. A two-dimensional surface such as that of a ball is curved and we
can see and understand it. The concept of curved three or four-dimensional
spaces are impossible to imagine what they really look like.
We already know that the Euclidean geometry is valid on the two-dimensional flat plane, but it is not anymore the case on a sphere although it is two-dimensional too but, in addition, also curved. Three-dimensional spaces are all non-Euclidean. According to Einstein, our three-dimensional space is curved and he showed that this is due to the gravitational fields of the massive bodies that are in the space. Around a massive object, the space is curved and its curvature -that is the degree its geometry deviates from that of Euclid- increases with the mass of the object. On earth this effect is small but in the space where we have massive bodies like planets, stars and galaxies the curvature of the space is important and cannot be neglected.
The classical concepts that space and time are absolute have been shown to be wrong by the general theory of relativity. All measurements of space and time are relative and depend on the velocity of the observer and the structure of space-time depends on the matter present. Space is curved at different degrees and time flows at different rates in different parts of the universe.
5.1 Special theory of relativity
The Dutch scientist Huygens developed the wave theory of light and in 1676 the Danish astronomer Olaus Roemer found that the light travelled at a finite, but very high speed. He noticed that the time between succeeding eclipses of each Jupiter's moons was not always the same. He postulated that this was due to the fact that the distance from Jupiter to the earth was not always the same. He concluded that the speed of the light was finite -if it was infinite the interval of time between the eclipses would be the same independently of the distance- and, knowing the variations in time and the distance to Jupiter he was able to calculate the speed of light. He did not get an accurate value because the distance between Jupiter was not known with accuracy but he got a reasonable value anyway (140,000 miles per second against the true value of 186,000).
In 1865 the British physicist James Maxwell unified the theories of the forces of electricity and magnetism. He showed that these forces did not result from particles acting on each other but were due to a field created around every electric charge and current. That single field carrying the electric and magnetic forces creates a force that acts on every current and charges in the vicinity. Since then it was clear that electricity and magnetism are aspects of the same force now known as electromagnetic force and the field as electromagnetic field. Disturbances in the electromagnetic field create waves that travel at the speed of light, very high but finite.
This was in contradiction with Newton's theory that there is an absolute standard of rest. If there is no such standard, then we cannot agree on any object's speed. As an example let us observe a ping pong game on a train travelling at 50 miles per hour. If a player hit the ball towards the head of the train with a speed of 10 miles per hour in relation to him. But to an observer on the platform the ball travels at 60 miles per hour. So what is the speed of the ball, 10 or 60 miles per hour? As we cannot define an absolute standard of rest, we cannot tell what is the absolute speed of the ball. Its speed depends on the frame of reference in which the speed is measured. According to Newton this was also true for the light, which we now know has a fixed speed. In order to combine Maxwell and Newton's theories, scientists introduced the notion of ether. This substance was assumed to be present everywhere, including in the vacuum such as in the empty space. Ether was the medium that carried electromagnetic waves just as air carries sound waves. Different observers would see light coming towards them with different speeds but in relation to the ether the speed of light was constant. In 1887, the Americans Albert Michelson and Edward Morley showed, experimentally, that the speed of light from the sun measured when the earth was going towards it or away from it was the same.
Albert Einstein in a famous paper written in 1905 showed -and this was confirmed a few weeks later by the French scientist Henri Poincaré- that ether was an unnecessary concept, that it did not exist, and that one had to abandon the concept of absolute time. To clarify this fact, let us take again the example of a train and two people, one on the train and one on the platform. Let us assume that the person on the train sends a flash of light from his torch on a distant wall. Both observers will disagree on the distance the light travels and, as the speed of light is the distance divided by the time, in order for both observers to find the same speed we must agree that the time it took for the light to hit the wall is also different for the two men. Time too, in relativity theory, is not absolute either. Einstein confirmed that the speed of light measured by observers moving at different speeds in different directions is the same.
Moreover, in relativity, time is not independent and separate from space but combines with it to form what is known as space-time continuum. In classical theory, three coordinates freely chosen describe the position of a point in space. In space-time, any event -anything happening in a specific point in space and at a certain time- is defined by four freely chosen coordinates, three spatial coordinates plus time, but there is really no difference between them. Another direct consequence of Einstein's theory of special relativity is the famous equation E = mc² (E is the energy, m the mass and c the speed of light). It allows us to calculate the amount of energy liberated if a mass m of matter is converted in electromagnetic radiation (that is what happens in atomic bombs). But it also tells us that if the energy of an object increases, so does its mass that, in turn, increases its resistance to acceleration (change of speed). As a result the faster an object moves, the higher its kinetic energy and the higher its mass. However, this increase in mass is only noticeable near the speed of light. The same equation shows that for an object to reach the speed of light an infinite amount of energy is required and, as this is impossible, no object can travel at the speed of light.
Einstein's special theory of relativity is incompatible with Newton's theory of gravity. Newton said that two objects are attracted by the force of gravity that depends only on their mass and the distance between them. Consequently, if one object is moved, the attraction changes immediately, implying that gravity waves have an infinite speed. Since the relativity theory tells us that the maximum speed is the speed of light, there is a contradiction between the two theories as far as gravity is concerned. It took Einstein until 1915 to propose a satisfactory explanation.
Albert Einstein enounced his theory of Special Relativity in 1905 but, for many years, not all scientists accepted it.
The main differences the Special Theory of Relativity and Newton's theory
can be described as follow:
- In the Newtonian or Euclidian theory, three coordinates can define the
position of any point in space and we are free to choose the coordinates
we want. However it is common sense that they should be chosen to describe
the problem in the best way. For instance we should not use the same coordinates
to describe the position of a point on top of a church or of a point on
the moon.
- In relativity an event always happens at a certain point in space and
at a certain time. Now to describe this event we need four arbitrary coordinates
instead of the previous three. Now there is no difference of principle between
the space and time coordinates. An event is now described in a four-coordinates
system called space-time. It is impossible to visualise a four-dimensional
space, but mathematics can deal with it.
5.2 General Theory of Relativity
In the special theory of relativity we assumed that there was a system of coordinates of reference K, whose condition of motion is such that the Galilean laws are valid in relation to it. A body not subject to any force will travel in a straight line. The laws of nature that are valid in K should also be valid in another system of coordinates K' if K' is moving uniformly on a straight line and without any rotation in relation to K. The principle of relativity was assumed to be valid for these reference-bodies of coordinates, but not for any other that move differently.
In general relativity all coordinate systems of reference (K, K', …) are equivalent for the description of natural events, and the general laws of nature are valid in all of them independently of their type of motion. It must be clear that the Galilean law does not hold in respect to coordinate systems that move in relation to each other in a non-uniform way.
5.2.1 Gravity
Any body such, as the earth, attracts any other body such as a stone. The
earth produces a gravitational field that attracts the stone making it fall.
We also know that the attraction of the earth decreases if the stone is
placed further away from it. Bodies that are moving under the influence
of a gravity field alone are accelerating. This acceleration does not depend
on the material or the physical state of the body. This explains why a piece
of lead and a feather fall exactly in the same way -same speed- in a gravitational
field (in vacuum or if we make a correction for the air resistance that
depends on the body) when they start from rest or from the same initial
velocity.
?
According to Newton's law of motion:
Force = (inertial mass)*(acceleration)
If gravitation is the cause of acceleration:
Force = (gravitational mass)*(intensity of the gravitational field)
Both inertial mass and gravitational mass are constant characteristics of the body.
From the two above equations we deduce:
Acceleration = (gravitational mass)*(Intensity of the gravitational field)/(inertial
mass)
?
We know from experience that the acceleration is the same for all bodies
in a given gravitational field and the acceleration is independent of the
nature and condition of the bodies. As a result the ratio of the gravitational
to the inertial mass must be the same for all bodies. By choosing the right
units this ratio is equal to one and this leads to the following:
The gravitational mass of a body is equal to its inertial mass
Einstein postulated that gravity is not an ordinary force. It was, as he saw it, a direct consequence from the fact that the space-time is not flat but curved or, better, "warped" by the mass and energy existing in it.
Let us consider a Galilean reference-body K, that is a domain with no gravity field. The behaviours of measuring-rods, clocks and "isolated" material points -moving uniformly and in straight lines- are known with reference to K from the special theory of relativity.
Now let us refer this domain to a random Gaussian co-ordinate system -a
non-rigid reference-body-, that is reference-body K'. In relation to K'
there is a gravitational field of a particular type that we will call G.
We learned the behaviour of measuring-rods, clocks, and free-moving material
points with reference to K' using mathematical transformation. At that point
we must make a hypothesis:
- The influence of the gravitational field G on the measuring-rods, clocks,
and free-moving material points continues to take place according to the
same laws, even when the gravitational field is not derivable from the Galilean
special case, simply by means of a transformation of co-ordinates.
We must analyse the space-time behaviour of the gravitational field G, derived from the Galilean special case by transformation of the co-ordinates. This behaviour takes the shape of a law that is always valid no matter how the non-rigid reference body is chosen. This is not yet the general law of the gravitational field since the gravitational field is of a special kind.
The general law-of-field of gravitation requires the generalisation of
the above law. To do this we must take into consideration the following
demands:
- The generalisation must satisfy the general postulate of relativity.
- If there is any matter in the domain, only its inertial mass and its energy
are of importance for their effect on the field.
- Gravitational field and matter together must satisfy the laws of conservation
of energy and of impulse.
The theory of gravitation derived in this way from the general postulate of relativity is simple, remove the defects of classical mechanics, interpret the empirical law of the equality of the inertial and gravitational mass and, in addition, helps explain some experimental results of observations made by astronomers that the classical mechanics could not.
If we apply this new theory to the cases where the gravitational fields are weak, and where the masses move with a speed low compared with the speed of light, then we fall back, in a first approximation, on the results of the Newtonian theory. But, in this case, the Newtonian theory is obtained without having to make any assumption (Newton had to assume that the force of attraction between two bodies in inversely proportional to the square of the distance separating them). If we increase the accuracy of the calculations made with the new theory then the deviations from the Newton theory are evident. In particular the general theory of relativity can explains why the orbit of the planet Mercury is not stationary by reference to the fixed stars, whereas the orbits of all the other planets are.
5.2.2 Heavy Bodies
From the general theory of relativity we deduce that bodies -such as the earth- are not moving on a elliptical orbit due to the force of gravity, but because they follow the equivalent of a straight path in a curved space. This path is known as "geodesic" and it is the shortest (or the longest) path between two points of the curved space. To explain in simpler way what a "geodesic" is, let us take the case of the surface of the earth, which is a two-dimensional curved space. The shortest distance between two points of the earth is on the great circle that joins them.
Bodies always follow geodesics in four-dimensional space-time but they appear curved to us living in our three dimensional space. It is, however, only an appearance. For instance, the earth follows a geodesic in four-dimensional space-time curved by the mass of the sun. To us, in our three-dimensional space, the orbit of the earth appears to be elliptical. In the absence of matter, geodesics in four-dimensional space-time correspond to straight lines in three-dimensional space. In the presence of matter, four-dimensional space-time is distorted and the paths of bodies appear to us in three-dimensional space as explained by the Newton theory based on gravity forces.
The orbits of the planets calculated by the General Theory of Relativity are quite close to those foreseen by the Newtonian Theory. The only exception is Mercury that, being the planet closest to the earth, is subject to a very strong gravitational force that put it on a rather elongated orbit. The General Theory predicts that the long axis of its orbit should rotate around the sun of about one degree in ten thousand years. The Newtonian Theory could not predict this.
5.2.3 Light Rays
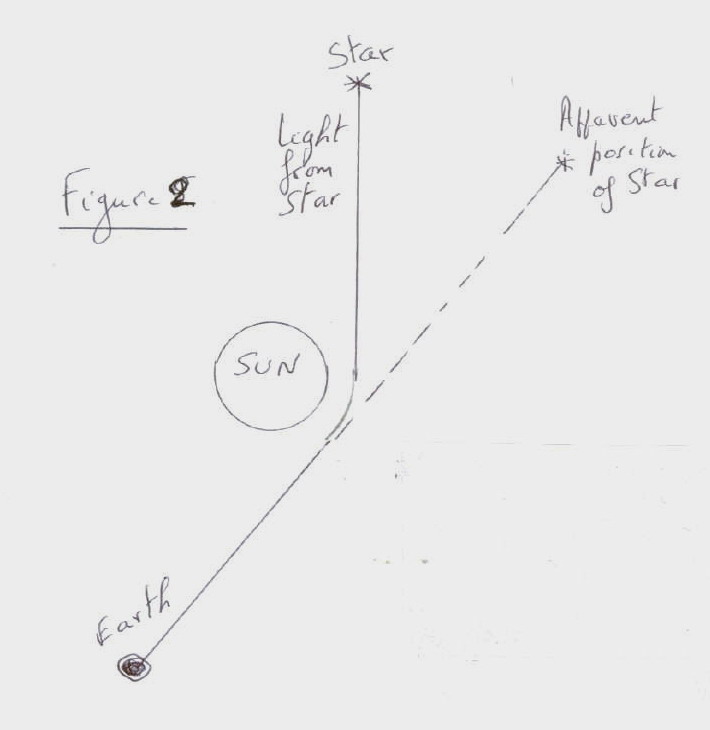
The light rays in space-time are also following geodesics. As space is curved for them too, to us, in three-dimensional space, it looks like light does not travel in straight line as gravitational forces bend it. A light coming from a far-away star passing near the sun will be deflected by a small angle, and now the star will appear in a different position to an observer on the earth (see figure 2). It is difficult to observe this effect as the sun is too bright but it can be done, and has been done, during an eclipse of the sun when the moon blocks the sunlight.
5.2.4 Time
General Relativity also predicts that time appears to run slower near a heavy body like the sun hat on the earth. This is due to the direct relationship between the energy of light and its frequency: the greater the energy, the greater its frequency. When we send a pulse of light upward in the earth gravitational field its energy decreases as it goes up as well as its frequency. An observer high up above would have the impression that everything on earth is taking a longer period of time to happen. This too has been experimentally tested.
This led to what has been described as the twin paradox. Let assume that one twin goes for a long journey in a space ship travelling at near light velocity. When he comes back he would be younger that his twin brother who remained on the earth.
Einstein explained this behaviour of time using the "Principle of Equivalence", the extension, in General relativity, of the fundamental postulate of Special Relativity. The fundamental postulate of special relativity says that the scientific laws should be the same for all freely moving observers, and this independently of the speed they are moving at. The principle of equivalence goes one step further and applies to observers who are not freely moving but are under the influence of a gravitational field. In summary, the principle of equivalence means that in small regions of space, it is impossible to tell if you are at rest in a gravitational field, or accelerating uniformly in space.
Let us now assume that a man is in a lift in space where there is no gravity and as a result, no "up" and no "down"; the man is floating freely as we have seen astronauts do. Let us start moving the lift with a constant acceleration, the man suddenly reacquires his feeling of weight, and distinguishes the floor from the ceiling of the lift. There too a ball left free would drop on the floor as it does on earth. In fact the man feels exactly the same way that he would feel in a stationary lift in a uniform gravitational field. Einstein realised that, as you cannot say if the train you are in is moving uniformly or is at rest, you cannot tell from inside the lift if it is accelerating uniformly or if it is in a uniform gravitational field. This is what the principle of equivalence means.
This is true only if the inertial mass (the mass in Newton's second law that allows to calculate the acceleration of a body subjected to a given force) and the gravitational mass (the mass in Newton's law of gravity) are the same. Fortunately this is the case and, as a result, all bodies fall at the same speed under the influence of gravity.
Let us assume that a very long rocket is floating freely in space. Its length is such that it takes light one second to go from top to bottom. At both ceiling and floor -at both ends- there is a man. The man at the ceiling send two light signals one second apart. The man on the floor receives them one second apart, but one second later. Let us now assume that the rocket is accelerating upward. The first signal has less distance to travel so it will arrive to the floor man less that one-second later. Due to the acceleration, the rocket is moving faster when the second signal is sent and it has even less distance to travel and the floor man will measure less than one second between the two signals (if the rocket is moving at a constant speed, that is not accelerating, the time between the two signals received by the floor man would still be one second). According to the principle of equivalence, this effect will apply if the rocket is sitting in any gravitational field -for instance on the rocket launching pad on earth. Newton would say that gravity has no effect, and if the same signals are sent one second apart from the ceiling, the floor man will receive them one second apart again. But according to the principle of equivalence of general relativity things are different. Here again the floor man will notice that the two signals reach him less that one second apart although the ceiling man sends them as before. What general relativity tells us is that time runs differently for observers in motion, it also runs differently for observers at different height in a gravitational field. In the above example, we can say that time moves more slowly closer to the earth's surface and the stronger the field the stronger the effect.
Newton's laws showed that there is no absolute space and now general relativity
shows that there is no absolute time.
5.2.5 Space-time continuum of the General Theory of Relativity compared
with the same continuum in the Special Theory
- Space-time continuum of the Special Theory of Relativity
We can now formulate more exactly the idea of Minkowski that we introduced
briefly before. In the special theory of relativity certain co-ordinate
systems are given preference for the description of the four-dimensional
space-time continuum, we called them "Galilean co-ordinate systems."
In these systems four coordinates x, y, z and t determine an event, in other
words a point, of the four-dimensional continuum. For the transition from
one Galilean system to another that is moving uniformly by reference to
the first, the equations of the Lorentz transformation are used.
Let us consider two events close to each other in the four-dimensional
continuum. The differences in their position in a Galilean system of coordinates
K are dx, dy, dz and dt. By reference to another Galilean system of co-ordinates
K' the differences are dx', dy', dz' and dt'. These intervals always follow
the condition:
dx²+dy²+dz²-c²dt² = dx'²+dy'²+dz'²-c²dt'²
The validity of the Lorentz transformation follows from this condition.
The distance ds between two points of the four-dimensional space-time continuum
can be expressed as ds²=dx²+dy²+dz²-c²dt²
And ds has the same value for all Galilean system of co-ordinates. If we replace x,y,z,sqrt(-1)*ct by x1,x2,x3,x4 we have: ds² = dx1²+dx2²+dx3²+dx4² that is also independent of the system of reference. We call ds the "distance" between two events or two four-dimensional points.
In consequence, if we choose as time-variable the imaginary term Sqrt(-1)*ct instead of the real value t, the space-time continuum -in special theory of relativity- is a "Euclidian" four-dimensional continuum.
- Space-time continuum of the General Theory of Relativity
We saw before that the velocity of light always depends on the co-ordinates
when a gravitational field is present. In other words, the presence of a
gravitational field invalidates the definition of the co-ordinates and the
time. As a result we must accept that the space-time continuum cannot be
regarded as Euclidian. It is impossible to build up a system, or reference
body, from rigid bodies and clocks so that measuring-rods and clocks, fixed
rigidly in relation to each other, indicate position and time directly.
To go over this problem, one must refer the four-dimensional space-time continuum in an arbitrary manner to Gauss coordinates. Let us assign to every point -event- of the continuum four numbers -co-ordinates- x1, x2, x3 and x4 that have no direct physical meaning but are used as numbering the points of the continuum in a definite but arbitrary manner. We must not even think of x1, x2, x3 as space co-ordinates and x4 as time.
Let us now consider a point that is in any type of motion. If this point existed only for an instant (without duration) then it would be described in space-time by four co-ordinates x1, x2, x3, x4. As it exists during a well-defined amount of time, it must be represented by an infinite number of very close co-ordinates to give continuity to its trajectory. Instead of a material point we now have a uni-dimensional line in the four dimensional continuum. Any other such lines in the continuum correspond to as many points in motion.
When two such lines cross each other, it means that these two lines, representing the motion of two points, have a set of co-ordinates x1, x2, x3, x4 in common. When we described the motion of a single material point relative to a system of reference we, in fact, described the encounter of this point with a particular point of the reference system. We must state the problem with different words but the principle is the same. For instance, a given time is the encounters of the hands of the clock with two well-defined points on the dial.
In conclusion, every physical description is made of a certain number of
statements, each of them being the space-time coincidence of two events
A and B. In term of Gaussian co-ordinates, each of these statements is expressed
by the agreement of their four co-ordinates x1, x2, x3, x4. The description
of the space-time continuum by means of Gauss co-ordinates replaces the
description with the aid of a body of reference. It is not linked to the
Euclidean character of the continuum that has to be represented.
5.2.6 Exact formulation of the General Principle of Relativity
Previously we provisionally defined the general principle of relativity
as follow:
"All bodies of reference K, K' etc., are equivalent for the description
of natural phenomena, whatever their motion."
This formulation has to be changed, as the definition of rigid-reference
bodies in the framework of the special theory of relativity, is generally
not possible in space-time concept. Here the gauss co-ordinate system must
replace the body of reference. In this view the general principle of relativity
becomes:
"All Gaussian co-ordinate systems are equivalent for the formulation
of the laws of nature.
We can now state the general principle of relativity in yet a more precise form. According to the special theory of relativity, the equations of the general laws of nature have the same form if we apply the Lorentz transformation to replace the space-time variables x, y, z, t of a Galilean reference-body K by the space-time variables x', y', z', t' of a new reference body K'.
According to the general theory of relativity, if we arbitrarily substitute the Gaussian variables x1, x2, x3, x4, the initial equations are changed into equations of the same form. In the old three-dimensional system of co-ordinates, the special theory of relativity deals with Galilean domains that are those where no gravitational field exists. In this case a Galilean reference-body serves as body of reference. This is a rigid body whose motion is such that the Galilean law of uniform rectilinear motion of isolated points is valid in relation to it.
Let us refer the same Galilean domains to non-Galilean reference-bodies. In this case a special gravitational field is present. In gravitational fields, the concept of rigid bodies with Euclidean properties does not exist anymore and so, in the general theory of relativity there is no such thing as a rigid body of reference. Clocks are also influenced by gravitational fields and the a physical definition of time obtained by using clocks has not the same meaning as in the special theory of relativity.
As a consequence non-rigid reference bodies are now used; their motion can be as varied as we can imagine and, moreover, their shape is also changing during their motion. All the same, clocks moving in any way are still used to define time. If all these clocks are fixed at different points on this non-rigid reference-body they will only satisfy one condition, that is, "the readings" observed simultaneously on adjacent clocks in space will only differ from each other by a infinitely small amount. This non-rigid reference-body is the main equivalent to a Gaussian four-dimensional co-ordinate system arbitrarily chosen. Every point on the non-rigid body is treated as a space-point, and every material point, which is at rest by reference to it, is considered to be at rest as long as the non-rigid body in considered as reference-body.
The general principle of relativity requires that all these non-rigid bodies
can be used as reference-bodies with equal right and equal success in the
formulation of the general laws of nature. In other words, the laws must
be independent of the choice of the non-rigid reference-body.