The Danish scientist Roemer was the first to show in 1676 that light travels at a finite but very high speed. In 1865, as a direct consequence of his research unifying the theories of the electrical and magnetic forces, a British physicist proposed the first known theory of the propagation of light. It was also discovered more or less at the same time that the velocity of light is the same for all colours. In addition the Dutch astronomer De Sitter showed that the light velocity does not depend of the speed of the body emitting the light.
As Newton had ruled out the concept of absolute rest, if light is travelling at a well-defined speed, it must be relatively to something. Scientists invented the notion of "ether" that was assumed to be present everywhere including empty space. In consequence light waves travel through ether in the same way that sound wave travel through air, its speed being relative to ether. All observers moving differently relative to ether would observe that light is reaching them at different speeds although its speed relative to ether remains constant.
As the earth is moving on an orbit around the sun, the speed of light measured in the direction of its motion should be higher that at right angle. Measurements made in 1887 by Albert Michelson and Edward Morley showed on the contrary that the speed of light was the same in both directions.
In 1905 Albert Einstein, soon followed by Henri Poincaré, showed that the concept of ether was not necessary if one discarded the notion of absolute time. Their theory of relativity required that the scientific laws should be the same for all observers moving at any speed.
From this one deduces that:
- Observers moving at different velocities will get the same value for the
speed of light.
- Nothing can travel faster than light.
From the famous Einstein equation E=mc² stating that energy and mass
are two aspects of the same thing (E = energy; m = mass; c - speed of light)
and the fact that nothing can travel faster than the speed of light, one
concludes:
- That energy is always required to increase the velocity of a body
- That to reach the speed of light, an infinite amount of energy is required
and, at that point, the mass of the body is infinite. This increase in mass
is only important at velocity near the speed of light. At 10% of c, the
increase in mass is only 0.5% while at 90% of c it is 90%.
- The ether does not exist and is not necessary.
In Newton's theory, if a pulse of light is sent between two points, different observers could agree on the time it takes to travel from one to the other -since time is absolute- but they would not agree on the distance travelled -space is not absolute. As the speed of light is equal to the distance travelled divided by the time it took, the different observers would find a different light speed. According to the theory of relativity, the speed of light is always the same. For all observers to get the same value for the speed of light both space and time measured by all the observers must be different or, in other words, both space and time are not absolute, and they are related to form what is described as "space-time".
At the beginning of the 20th century there were two theories about light:
- The particle theory favoured by Newton.
- The wave theory accepted by most scientists of the time.
- In fact, it was shown later on, both theories are correct; light can be
described both as wave and particle. Under the wave theory it is not clear
how light could be affected by gravity, but under the particle theory things
become clearer as all particles are affected by it.
Let us consider a rocket shot vertically from the earth surface. Usually it will reach a certain altitude then falls back on the earth. However if the rocket speed is high enough, it will escape into space. The minimum speed for this to happen is called "the escape velocity". If we replace the earth by a star, the escape velocity will depend on the gravitational field of this specific star. More massive stars have a higher escape velocity than small ones. After it was shown that light has a large, but finite speed, it was obvious that gravity affects light too. If the star is massive enough, its escape velocity will be higher that the speed of light and any light emitted by that star will be unable to escape and will fall back on it. These stars are called "Black Holes". Robert Oppenheimer used Einstein's general theory of relativity to explain, in 1939, how gravity affects light.
The gravitational field of the stars changes the paths of light rays passing close to them. We already know that closer stars are bending inward light rays emitted by faraway stars. This phenomenon was observed during eclipses of the sun. If a star contracts, the gravitational field on its surface increases and it bends more any light ray passing close by. If the star goes on shrinking in size, its gravitational field could eventually become so strong that the light rays are bend so much that they cannot escape anymore and, as nothing can travel faster that light, nothing else can escape that star's gravitational field. That star has created a region known as a black hole whose outer boundary is called "the event horizon". We know now that black holes are numerous in the universe.
The notion of "simultaneity" of two events is not as simple as it was thought until the beginning of the 20th century. Let us again consider a traveller in a train travelling at the speed v and a man standing still on the embankment. Let us also assume that lighting hits the rails at exactly the same moment at two distant points A and B. Let us call M the middle point between A an B. Our man on the embankment Stands in M with tools allowing him to see the points A and B at the same time. If he notices the two flashes of lightning at the same time then, for him they are simultaneous. This is due to the fact that the light takes the same time to travel from A to M that it takes from B to M.
Now let us consider a system of coordinates linked to our train travelling at a constant speed V along the rails. Will the traveller on the train sees the two strokes of lighting as simultaneous as they were for the man on the embankment? We will call M' the mid-point between A and B seen on the train. We will further assume that when the flashes of lightning occur M' coincides with M but, we must remember, that the train moves forward with the speed V. Our traveller is sitting at M' when the flash happens. If the speed of the train was V=0 then he would see the two flashes at the same moment like the man immobile on the embankment. But the train moves with the velocity V towards the flashes coming from B and away from the flash in A with the same velocity. It is obvious that the traveller will see the flash from B before he sees the one from A. Our train traveller, by reference to the system of coordinates linked to the train, will then conclude that the flash from B occurred before the flash of A. For him, the two flashes are not simultaneous like they were for the man on the embankment. In conclusion every system of coordinates has it own time or, in other words, time is different for different systems of coordinates. Time is not absolute.
In the same way the distance measured between two points A and B -for instance A in the middle of the first carriage and B in the middle of the last one- on a train travelling at a speed V, -by reference to a system of coordinate fixed to the train- is not the same that the distance measured by reference to a system of coordinates linked to the embankment (that is to the earth). In conclusion, the distance between the points A and B is not the same if measured by reference to the train or to the embankment.
The apparent incompatibility, in classical mechanics, between the principle
of relativity and the constant speed of light is due to the two following
classical assumptions:
- The time between two events is independent of the speed of the coordinates
of reference.
- The distance between two points on a rigid body does not depend on the
motion (speed) of the body of reference.
If we drop these two assumptions then the incompatibility disappears. Let
us come back to our example of a traveller in a train running at a speed
V while a man stands immobile on the embankment. But now we associate a
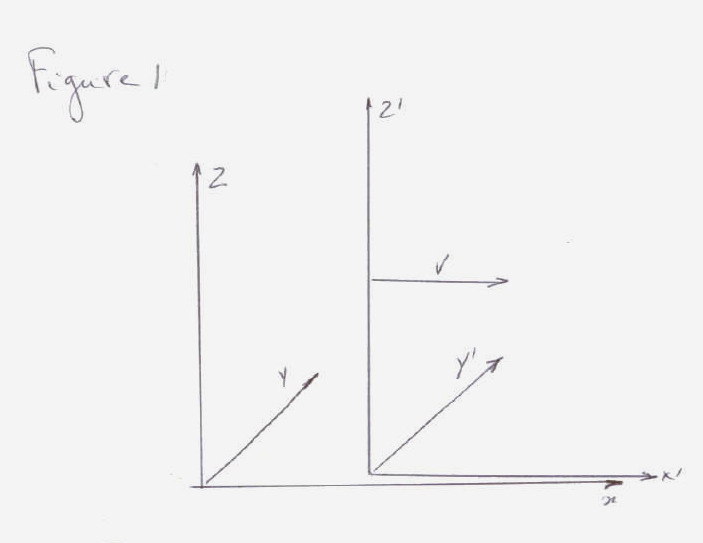
system K of four coordinates (x,y,z,t) linked to the embankment and another
K' (x',y',z',t') linked to the train. We want to know the coordinates x',y',z'
and t' of an event with respect to K', knowing the coordinates x,y,z, and
t of the same event relative to K.
?
The details of the calculations of what is known as the "Lorentz Transformations"
are given in annex 6.
For two systems of coordinates moving as indicated in figure 1 we have:
X' = (X - vt)/sqrt(1 - v²/c²)
Y' = Y
Z' = Z
T' = (t - vX/c²)/sqrt(1 - v²/c²)
The law of light transmission is satisfied for both coordinates K and K'.
If we send a light signal along the X-axis of K we have:
X = ct but in relation to K' it is:
X' = (c - v)t/ sqrt(1 - v²/c²) = ct'
t' = (1 - v/t)t/sqrt(1 - v²/c²)
But the speed of light is still c.
NB: The classical laws would have led to the following equations known as
the "Galilei Transformation". They can be obtained from the Lorentz
transformation above by making the speed of light c infinite (c = ):
X' = X -vt
Y' = Y
Z' = Z
t' = t)
?